I am conducting a exploration of reinforcement learning and what it means to us mere mortals. I will keep the mathematics light in the first couple of blog posts, and then ramp this up when we are comfortable with the concepts discussed.
What is Reinforcement Learning (RL)?
Imagine you are learning by trial and error: you try something, see what happens, learn from what worked (or did not work!) and adjust accordingly next time. That’s basically the idea behind reinforcement learning, obviously us mortals have to make it more complex, because that is what we do, but it is really that simple. To further explain, in RL we:
- We have an agent – the thing that makes decisions (e.g. a robot, a game playing program, a character in a game, a person in a hospital, etc.)
- The agent operates inside an environment – a world or context where the agent’s actions have consequences (e.g. the room the robot vacumn is cleaning, a level in a game, an obstacle course a vehicle has to navigate over, a road a car is driving on)
- The agent can take actions. After each action, the environment gives feedback: a reward (which might be positive or negative), and possibly changes the situation (state) for the next round.
- Over time, by repeating this cycle –> action –> feedback –> new action – the agent learns which actions tend to lead to better rewards overall. That is, the agent learns what “works” (and what doesn’t) in that specific environment.
In short: RL is learning by doing – not by being fed correct answers up front (as in supervised learning), but by trying, making mistakes, and adjusting behaviour over time.
“An RL-agent learns to make decisions by interacting with its environment”
This iterative cycle is detailed in this iterative flow:
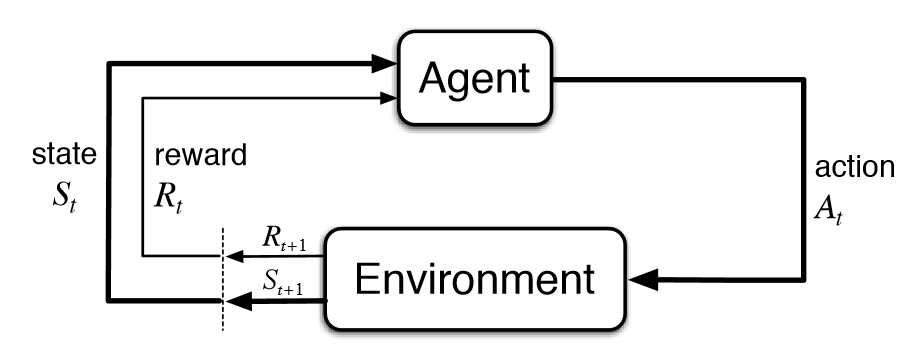
To get to understand how this process is calculated, we will focus on the Bellman Equation, which we will look at in the following section.
The Bellman Equation – the way I wish it was explained to me
There are many attempts at getting this right, without delving too deeply into the mathematics, that people retreat. I have found it is best to convey the idea analogously and then add the maths in gently. I hope I manage to achieve that here?
Firstly, let’s have a look at the full equation (and promise not to get intimidated at this point):
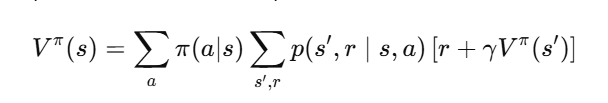

We will break down this process in a stepwise, and simple way.
Thought experiment: making a big decision
Imagine you’re learning to make a big decision – like choosing a career, picking which fund to invest in or learning a video game.
Some of the choices you make give good results immediately, others pay off later and some look good now, but hurt you afterwards. This is the exact situation learning agents face.
The Bellman equation is simply a way of saying:
The value of a situation = what you get now + what you can expect later
At its heart, this equation links present reward and future reward. Let’s analogise this.
Analogy 1: Should I Move Into This Room (Video Game)
Imagine a game where each room gives you:
- treasure (reward now)
- and leads to other rooms (future opportunities)
If you ask how good is this room overall? You must consider:
- How much treasure is here now
- How good the next rooms are
If the next rooms are safe, this room is good even if it has little treasure. However, if the next rooms are dangerous, this room is bad even if it has a lot of treasure.
This is exactly what the Bellman equation formalises. If I had to sum it up in once sentence:
A state is valuable if it leads to lots of reward – now and later.
Let’s explain the key symbols in the big scary equation in simple, plain English:

To sum this up it links: state –> reward + new state –> repeat, as the major steps of the process and the key links back into the Bellman equation.
To concrete this, we will do an analogy of walking on a trail through terrain.
Analogy 2: Walking on a Trail
You are hiking, and at each step:
- you enjoy the view (the current reward)
- and you move to a new viewpoint (future reward)
You’re trying to judge how good is this trail overall? So you look at:
- How much you enjoyed this step
- How much you expect to enjoy the remaining trail
This is where the Bellman equation shines, and why it was formulated.
Why any of this matters?
The Bellman equation is important because:
- It breaks a big problem (what’s the total future reward?)
- Into a small repeating step (reward now + value of the next step)
This simple recursion makes it possible for RL algorithms to learn:
- by bootstrap random sampling (taking random samples of a data point – with replacement – so the original samples get put back into the original pot of samples)
- by updating their values one step at a time
- without needing to simulate the entire future perfectly.
This is the foundation for all the other methods we will look at in this blog series:
- Q-Learning
- Deep Q Networks (DQN)
- Actor Critic Methods
- PPO (policy optimization used by OpenAI to improve their language models by ranking the responses from the decoder only model)
- Almost all of reinforcement learning
Now that we have all of the fundamentals in place – we will focus on the hiking scenario in the next blog post.
